Reverse vs Forward KL

17 December 2017

Consider

• \(q_\phi(x)\), a probability density of \(x\), parametrized by \(\phi\), and
• \(p(x)\), a probability density of \(x\).

Then

• If we minimize the \(\KL{q_\phi}{p}\) (or the reverse/exclusive KL) with respect to \(\phi\), the zero-forcing/mode-seeking behavior arises.
• If we minimize the \(\KL{p}{q_\phi}\) (or the forward/inclusive KL) with respect to \(\phi\), the mass-covering/mean-seeking behavior arises.

Gaussian Example

Let \begin{align} p(x) = \sum_{k = 1}^K \pi_k \mathrm{Normal}(x; \mu_k, \sigma_k^2) \\
q_{\phi}(x) = \mathrm{Normal}(x; \mu_q, \sigma_q^2), \end{align} where \(K = 2\), \(\pi_k = 0.5, \sigma_k^2 = 1\) (\(k = 1, 2\)), \(\mu_1 = 0\), \(\mu_2\) is increasing from \(0\) to \(10\) and \(\phi = (\mu_q, \sigma_q^2)\).

The behavior of minimizing the forward and reverse KL divergences with respect to \(q_{\phi}\) is as follows:

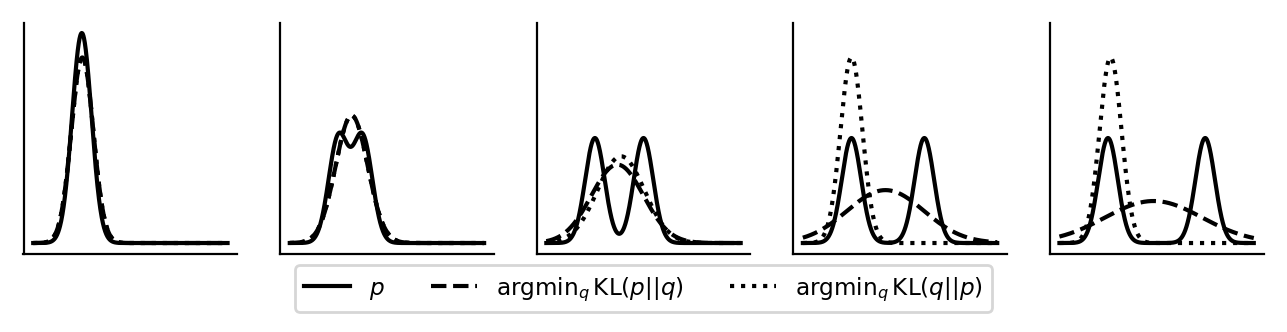
Intuitive explanations and speculations for the origins of the various terms:

Reverse KL: Zero-Forcing/Mode-Seeking

The terms mode-seeking and zero-forcing for minimizing the reverse KL comes from the fact that this minimization forces \(q_{\phi}\) to be zero where \(p\) is zero and hence makes it concentrate on one of the modes (last two plots). While the zero-forcing behavior can be explained by looking at the expression for the reverse KL divergence (when \(p\) is (almost) zero and \(q_{\phi}\) is non-(almost) zero, this KL is (almost) infinity), the mode-seeking behavior is only a corollary of the zero-forcing behavior which doesn’t need to always occur. For example, note that in the second and third plots, there are two modes but \(q_{\phi}\) is not mode-seeking because there wasn’t an (almost) zero between the modes. The reverse KL is called the exclusive KL because it exludes a mode.

Forward KL: Mass-Covering/Mean-Seeking

Since there is a \((\log p(x) - \log q_{\phi}(x))\) term in the forward KL, to make this term small, we must make sure that there is some mass under \(q_{\phi}\) wherever there is some mass under \(p\). We can see this in all the plots. This is where the term mass-covering comes from. The term mean-seeking is merely to contrast with mode-seeking. The term inclusive KL is to contrast with exclusive KL.

For more detailed intuitions, check out this blog post and Wittawat’s comment. For more detailed treatment, check out the references.

---

References

1. Minka, T., & others. (2005). Divergence measures and message passing. Technical report, Microsoft Research.
   • Bib

   @techreport{minka2005divergence,
     title = {Divergence measures and message passing},
     author = {Minka, Tom and others},
     year = {2005},
     institution = {Technical report, Microsoft Research}
   }
   

2. Turner, R. E., & Sahani, M. (2011). Two problems with variational expectation maximisation for time-series models. Cambridge University Press.
   • Bib

   @incollection{turner2011two,
     title = {Two problems with variational expectation maximisation for time-series models},
     author = {Turner, RE and Sahani, M},
     year = {2011},
     publisher = {Cambridge University Press}
   }
   

[back]