Amortized Inference

19 December 2017

Consider a probabilistic model \(p(x, y)\) of \(\mathcal X\)-valued latents \(x\), \(\mathcal Y\)-valued observes \(y\). Amortized inference is finding a mapping \(g_\phi: \mathcal Y \to \mathcal P(\mathcal X)\) from an observation \(y\) to a distribution \(q_{\phi}(x \given y)\) that is close to \(p(x \given y)\). Let’s go with the following objective that is to be minimized: \begin{align} \mathcal L(\phi) = \int \overbrace{w(y)\pi(y)}^{f(y)} \, \mathrm{divergence}\left(p(\cdot \given y), g_\phi(y)\right) \,\mathrm dy. \label{eqn:amortization/objective} \end{align}

Here,

• \(\mathcal L\) is the objective function,
• \(\pi(y)\) is some distribution over \(y\) values we are interested in performing good inference during test-time,
• \(w(y)\) is a weighting for each \(y\),
• \(f(y) := w(y)\pi(y)\) is just grouping the two together, and
• \(\mathrm{divergence}\) measure a distance between two probability distributions (see Wikipedia).

Variational Inference

The objective we are minimizing is \begin{align} \mathcal L(\phi) = \int p(y) \underbrace{\left[\KL{q_{\phi}(\cdot \given y)}{p(\cdot \given y)} - \log p(y)\right]}_{-\mathrm{ELBO}(\phi, \theta, y)} \,\mathrm dy. \label{eqn:amortization/vae-objective} \end{align} Call this the \(qp\) loss. This objective is also suitable for simultaneous model learning.

Inference Compilation

The objective we are minimizing is \begin{align} \mathcal L(\phi) = \int p(y) \, \KL{p(\cdot \given y)}{q_\phi(\cdot \given y)} \,\mathrm dy. \end{align} Call this the \(pq\) loss.

Examples

Let’s compare these two losses on a sequence of increasingly difficult generative models.

Gaussian Unknown Mean

The generative model: \begin{align} p(x) &= \mathrm{Normal}(x; \mu_0, \sigma_0^2) \\
p(y \given x) &= \mathrm{Normal}(y; x, \sigma^2). \end{align} In the experiments, we set \(\mu_0 = 0\), \(\sigma_0 = 1\), \(\sigma = 1\).

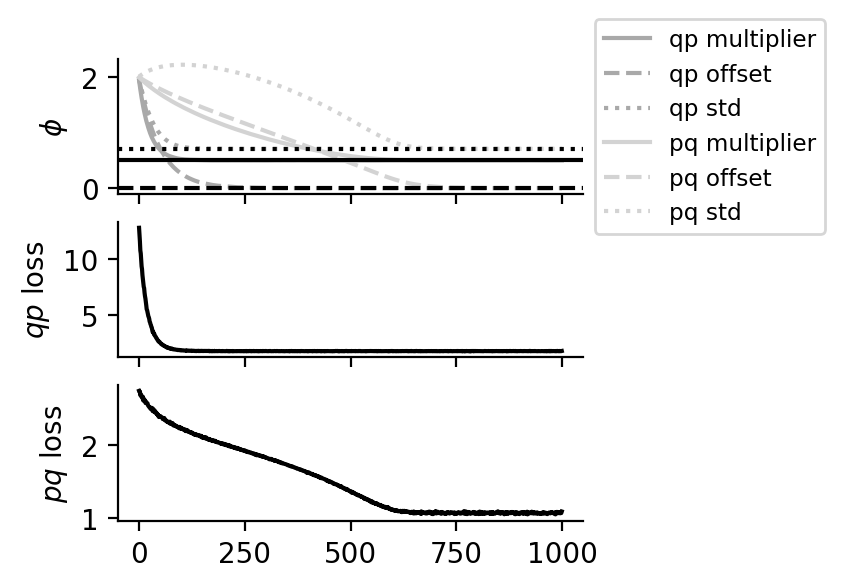
The inference network: \begin{align} q_{\phi}(x \given y) = \mathrm{Normal}(x; ay + b, c^2), \end{align} where \(\phi = (a, b, c)\) consists of a multiplier \(a\), offset \(b\) and standard deviation \(c\).

We can obtain the true values for \(\phi\): \(a^* = \frac{1/\sigma^2}{1/\sigma_0^2 + 1/\sigma^2}\), \(b^* = \frac{\mu_0/\sigma_0^2}{1/\sigma_0^2 + 1/\sigma^2}\), \(c^* = \frac{1}{1/\sigma_0^2 + 1/\sigma^2}\).

Amortizing inference using both the \(pq\) and the \(qp\) loss gets it spot on.

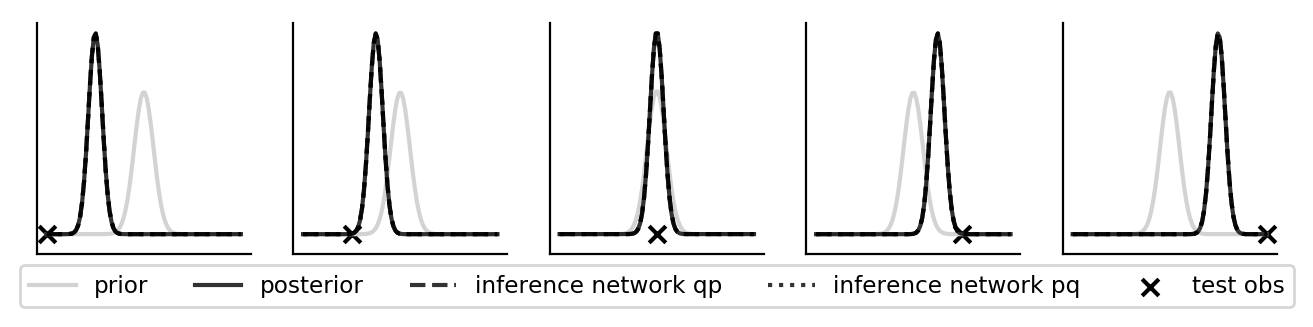
Gaussian Mixtures

The generative model: \begin{align} p(x) &= \sum_{k = 1}^K \pi_k \mathrm{Normal}(x; \mu_k, \sigma_k^2) \\
p(y \given x) &= \mathrm{Normal}(y; x, \sigma^2). \end{align} In the experiments, we set \(K = 2\) and \(\mu_1 = -5\), \(\mu_2 = 5\), \(\pi_k = 1 / K\), \(\sigma_k = 1\), \(\sigma = 10\).

The inference network: \begin{align} q_{\phi}(x \given y) &= \mathrm{Normal}(x; \eta_{\phi_1}^1(y), \eta_{\phi_2}^2(y)), \end{align} where \(\eta_{\phi_1}^1\) and \(\eta_{\phi_2}^2\) are neural networks parameterized by \(\phi = (\phi_1, \phi_2)\).

Amortizing inference using the \(pq\) loss results in the mass-covering/mean-seeking behavior whereas using the \(qp\) loss results in zero-forcing/mode-seeking behavior (for various test observations \(y\)). The zero-forcing/mode-seeking behavior is very clear in the second plot below: \(\eta_{\phi_1}^1\) always maps to either \(\mu_1\) or \(\mu_2\), depending on which peak is larger; \(\eta_{\phi_2}^2\) always maps to more or less a constant. It is also interesting to look at \(\eta_{\phi_1}^1\) and \(\eta_{\phi_2}^2\) when the \(pq\) loss is used to amortize inference. It would actually make more sense if \(\eta_{\phi_2}^2\) dropped to the same value as \(\eta_{\phi_2}^2\) in the \(qp\) case.

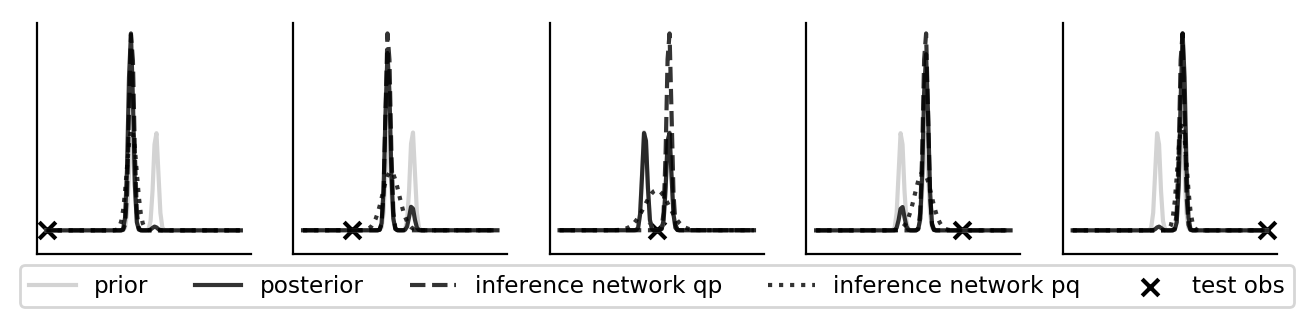
Gaussian Mixtures (Non-Marginalized)

The generative model: \begin{align} p(z) &= \mathrm{Discrete}(z; \pi_1, \dotsc, \pi_K) \\
p(x \given z) &= \mathrm{Normal}(x; \mu_z, \sigma_z^2) \\
p(y \given x) &= \mathrm{Normal}(y; x, \sigma^2). \end{align} In the experiments, we set \(K = 2\) and \(\mu_1 = -5\), \(\mu_2 = 5\), \(\pi_k = 1 / K\), \(\sigma_k = 1\), \(\sigma = 10\).

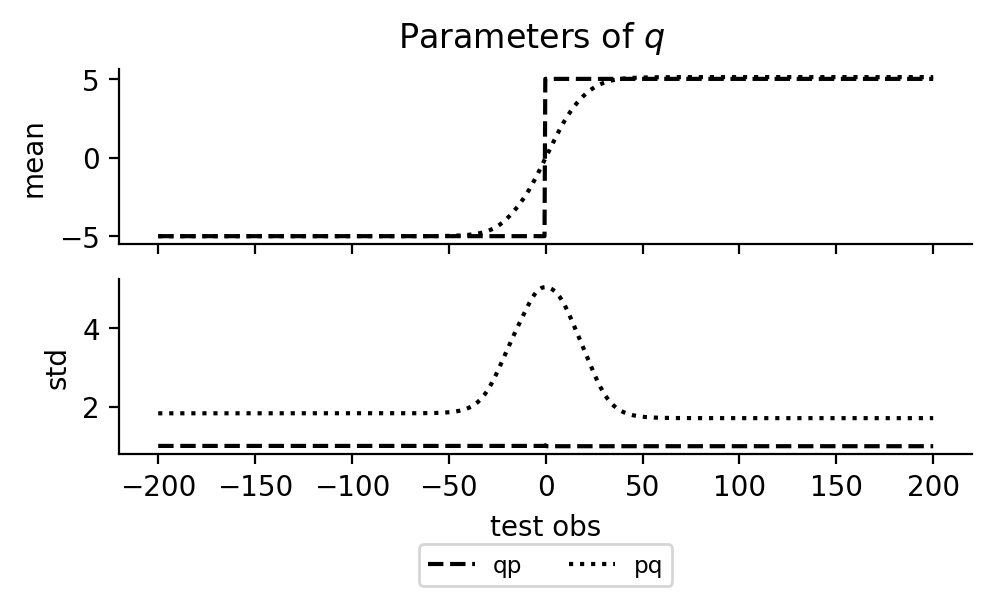
The inference network: \begin{align} q_{\phi}(z \given y) &= \mathrm{Discrete}(z; \eta_{\phi_z}^{z \given y}(y)) \\
q_{\phi}(x \given y, z) &= \mathrm{Normal}(x; \eta_{\phi_\mu}^{\mu \given y, z}(y, z), \eta_{\phi_{\sigma^2}}^{\sigma^2 \given y, z}(y, z)), \end{align} where \(\eta_{\phi_z}^{z \given y}\), \(\eta_{\phi_\mu}^{\mu \given y, z}(y, z)\), and \(\eta_{\phi_{\sigma^2}}^{\sigma^2 \given y, z}\) are neural networks parameterized by \(\phi = (\phi_z, \phi_\mu, \phi_{\sigma^2})\).

In the first plot below, we show the marginal posterior \(p(z \given y)\) and \(p(x \given y)\) and the corresponding marginals of the inference network. The posterior density is approximated as a kernel density estimation of resampled importance samples. In the second plot below, we show the outputs of the neural networks for different inputs.

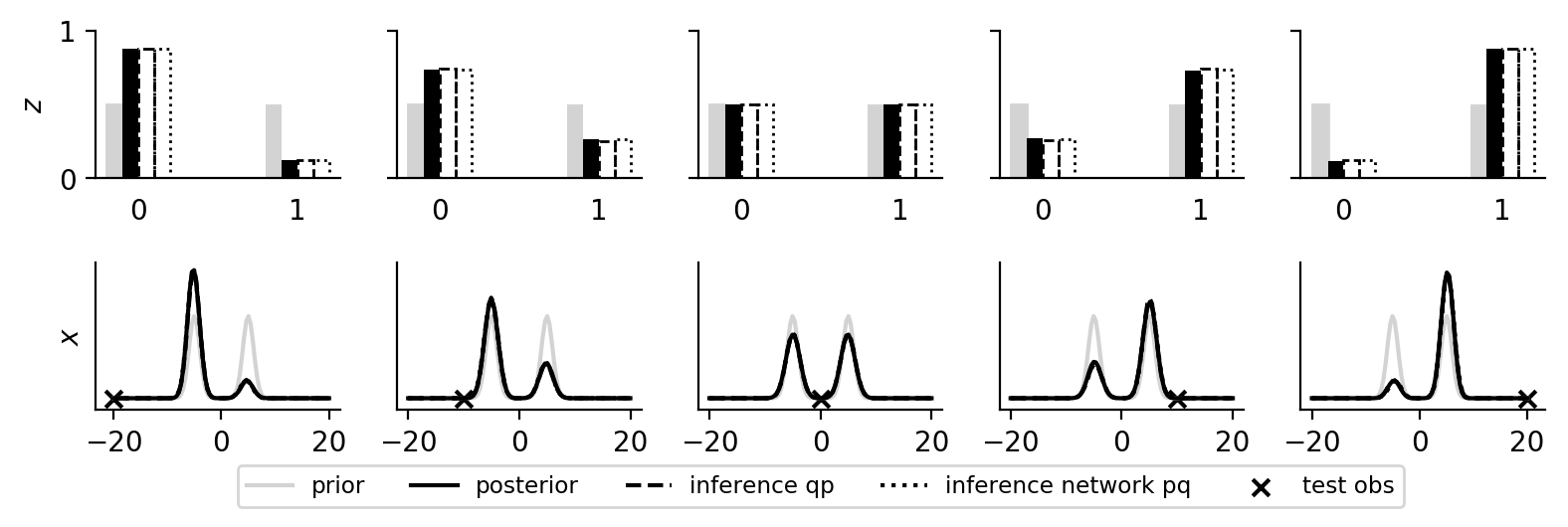
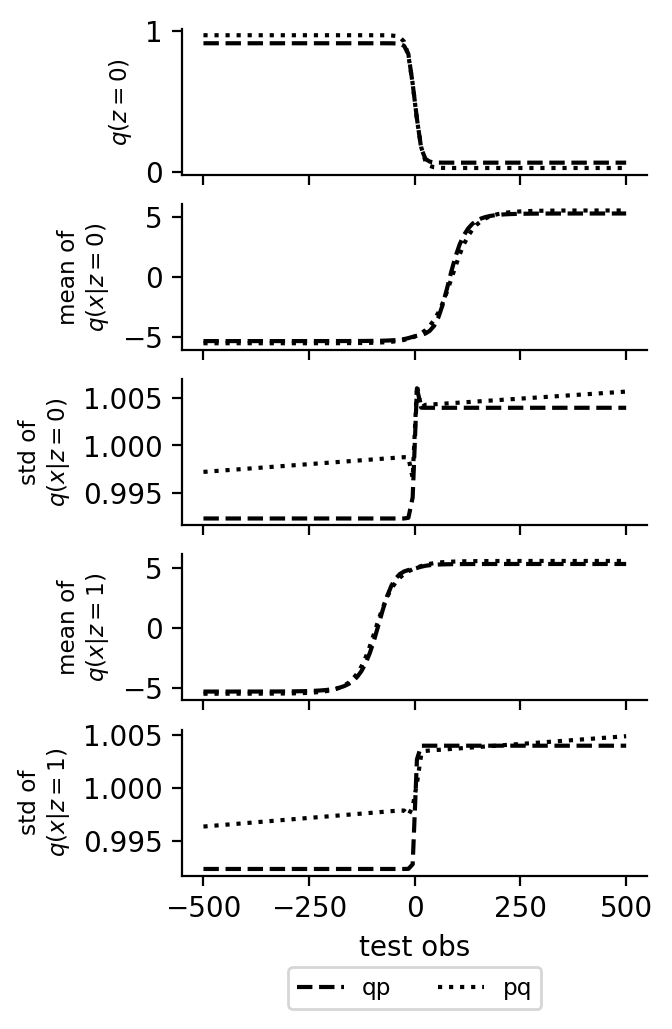
Gaussian Mixtures (Open Universe)

Generative model:

• \(K \sim \mathrm{Discrete}(\alpha_1, \alpha_2) + 1\).
• if \(K = 1\):
  • \(x \sim \mathrm{Normal}(\mu_{1, 1}, \sigma_{1, 1}^2)\).
• else:
  • \(z \sim \mathrm{Discrete}(\pi_1, \pi_2)\).
  • if \(z = 0\):
    • \(x \sim \mathrm{Normal}(\mu_{2, 1}, \sigma_{2, 1}^2)\).
  • else:
    • \(x \sim \mathrm{Normal}(\mu_{2, 2}, \sigma_{2, 2}^2)\).
• observe \(y\) under \(\mathrm{Normal}(x, \sigma^2)\).

The inference network:

• \(K \sim \mathrm{Discrete}(\eta_{\phi_1}^1(y)) + 1\).
• if \(K = 1\):
  • \(x \sim \mathrm{Normal}(\eta_{\phi_2}^2(y, K), \eta_{\phi_3}^3(y, K))\).
• else:
  • \(z \sim \mathrm{Discrete}(\eta_{\phi_3}^3(y, K))\).
  • if \(z = 0\):
    • \(x \sim \mathrm{Normal}(\eta_{\phi_4}^4(y, K, z), \eta_{\phi_5}^5(y, K, z))\).
  • else:
    • \(x \sim \mathrm{Normal}(\eta_{\phi_4}^4(y, K, z), \eta_{\phi_5}^5(y, K, z))\).

In the plot below, we can see that the inference network learns a good mapping to the posterior (tested on various test observations).

---

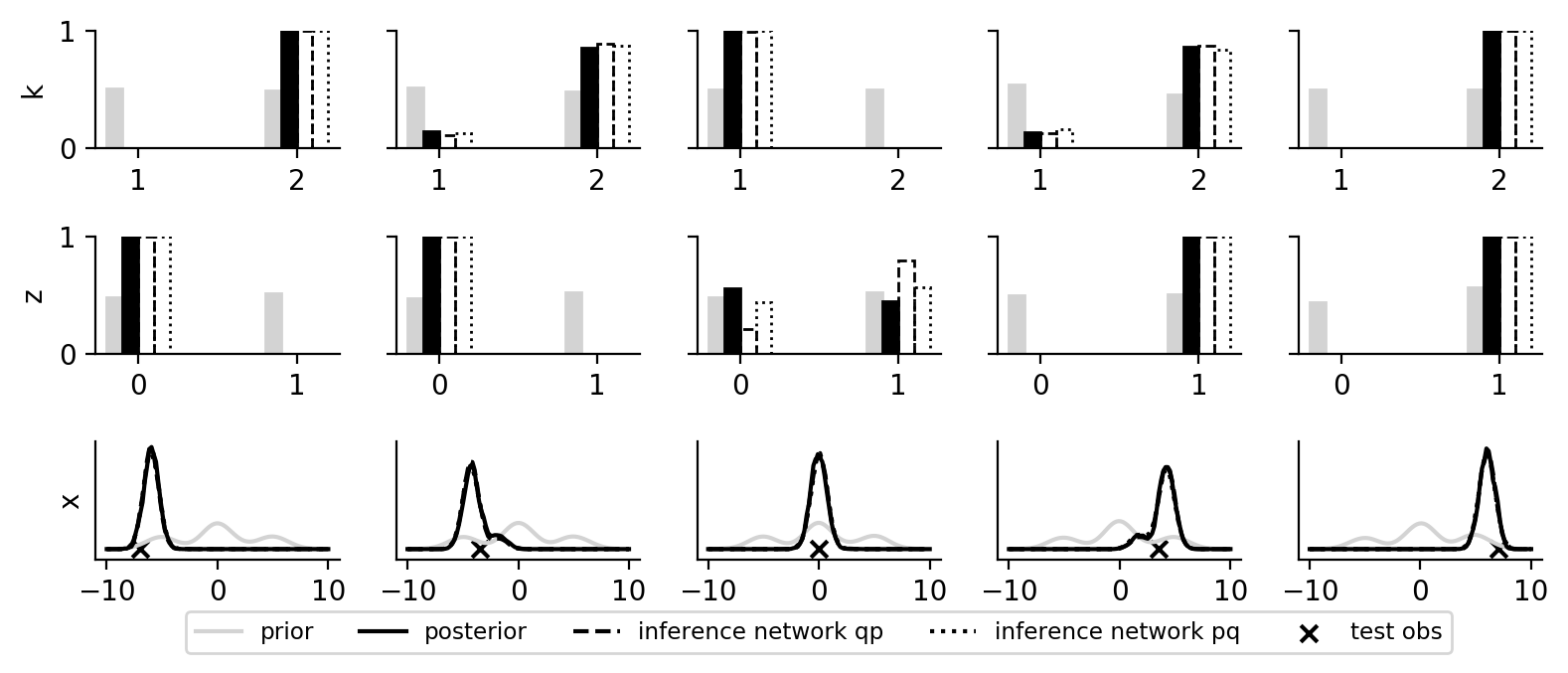
References

[back]